The Most Beautiful Equations

Sometimes mathematics is beautiful. It's a hard thing to observe; you need to peer through various mystifying levels of symmetries and distractions, until you finally arrive at that most elusive moment where you suddenly realise it's all really simple.

Many of the greatest equations, theories and postulates have relied on the power of their beauty. Einstein's E=mc² has entered the public consciousness like no other, while many others intrigued and delighted the scientific community without much publicity.

Gauss
Gauss's integral for example, reduces this technically baffling integral to a silly and simple number - albeit one which goes on forever.. 1.772453850905516027298167483314...

Comprehending the lateral method used to solve this problem was a major moment in my scientific education. The solution appears to be infinitely unsolvable, if you think of 'x' being a straight line, which as far as any really grasped, was mostly what integration seemed to be about.

However, if you instead think of this problem in two equal dimensions, you can bend the co-ordinates into a circle. Suddenly, as the circle closes, the difficult bit drops off and you can solve the bugger easily to get 1.77...

This identity is used heavily in quantum mechanics, in fact - the whole field is underpinned by the kind of logic used in this solution.

Euler

Euler also used circles to describe other strange and useful numbers. Imagine a second hand travelling round the clock face. Imagine a straight line drawn from 9 to 3. The question is, how far away from that line is the tip of the second hand, as it travels round? If you plot a graph of that distance against time, you'll get a sine wave:



If you instead imagine a straight line between 12 and 6, and plot that, you'll get the same thing, except the start point will be a quarter of a circle further round. These two waves, one '3 hours' out of phase with the other, are called sin and cos.

We would usually use an angle called a radian instead of the clock metaphor. A clock has 12 hours, a circle has 2π radians - twice the number π. So the two waves are π/2 ( 2π / 4 ) out of phase, and the two waves are sinθ and cosθ where θ revolves all the way around from 0 to 2π, like the hand making a full revolution.

Euler showed us that you can treat sin and cos as really the same things, if you use something called an imaginary number.

Okay, I'm thinking of a number. What is it? "Well.. " you say, "it could be anywhere between zero and infinity!" What about negative numbers? "Well, minus infinity to infinity then!".

And you'd have me there. But suppose instead I was thinking of the square of a number, there'd be no point guessing a negative number because any number, positive or negative, gives you a positive number when you square it. In fact, if someone claims they've thought of one, well, it can't be real can it? No real numbers do that! Must be some kind of.. imaginary number, hah!

In mathematics, existing and being real thankfully don't have to mean the same thing, so we can imagine numbers which exist but aren't real. They'll actually really useful, and in fact have a lot to do with circles, and waves, and lots of really geeky physics stuff.


Don't worry if that's a bit confusing, The point is, when you combine in the radian idea, the sin and cos, the imaginary number idea, and the exponential (I won't go into that here - check the link at betterexplained.com) you arrive at the most startlingly simple statement:

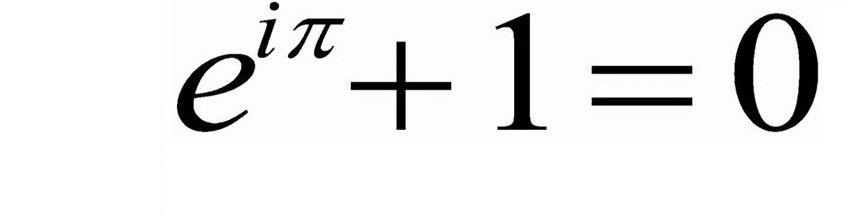This, I believe, is the most beautiful equation. The soaring exponential, the elusive imaginary, the reliable circle, the triumphant '1', then equality to nothing. It's the poetry of the universe, and it's just the first line.